在前幾天我們看到了關於房價預測的線性迴歸問題，接著提到如何定義模型、判斷好壞、更新模型。在這一篇文章我們會實際以 Python 跑過一次線性迴歸。

在開始之前

接下來的實作建議在 jupyter notebook 或是 Google Colab 當中運作會比較方便。

在接下來的實作我們會需要

• python3
  我使用的是 3.10 這個版本
• numpy
• matplotlib

如果你還沒安裝這些，建議可以選擇到 Google Colab 上運行。

開始實作吧！

首先我們的資料 分別以 numpy array 表示如下，並且取得資料的數量 。

import numpy as np
x = np.array([498, 523, 550, 834, 980, 1250, 1430, 1700, 1780, 1900, 2100])
y = np.array([100, 150, 200, 210, 300, 290, 340, 293, 350, 290, 285])
n = len(x)

之所以在這裡不是用一般的 list 而是 numpy array 是因為待會我們要對它做運算，例如加法和乘法。因為期待加法和乘法能夠是一一對應每個元素操作，所以用一般的 list 是不行的。

之前提過機器學習的三個步驟

1. 定義函數
2. 將資料輸入進模型，並評估模型好壞
3. 調整參數大小

定義函數、Loss Function

首先我們定義 這樣的函數。接下來評估好壞的 Loss Function 設定成小修改後的 MSE。

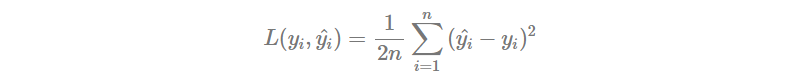
def Loss(y, y_pred):
    return np.sum((y - y_pred) ** 2) / (2 * n)

設定 Hyperparameters

最後在調整參數的部分需要設定 參數初始值 以及 Learning Rate 。這裡我們分別設定 。

至於更新到甚麼狀態下需要停下來，理想上當然會是期待斜率為 0 的時候停下，不過在實作上這種狀況可說是幾乎不會遇到，所以更多情況是設定一個 epoch ，也就是經過多少輪更新後會停下來。這裡我們先設定 1000 個 epoch。

lr = 0.000001
epochs = 1000
a, b = 0, 0

更新參數

更新參數的部分就會是有一個迴圈，每次我們會先計算出模型的輸出 ，或是我在 code 當中的 y_pred。

y_pred = a*x + b

接下來透過剛剛實作的 Loss 函數取得整體的 Loss，讓我們可以進一步評估模型更新的狀況。

loss = Loss(y, y_pred)

再來就是要取得兩個參數的偏微分了！回顧一下昨天的推導過程。

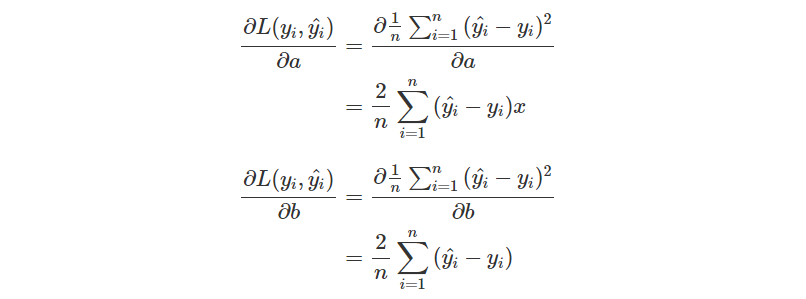
不過我們有稍微修改了一下 Loss Function，所以會少掉前面的 2 倍，也就是

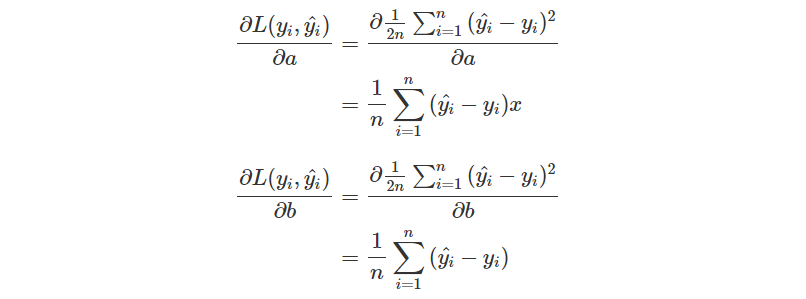
因為我們使用了 numpy array，所以一切操作就會簡單許多。

• +, -, *, / 的操作都會自動對應元素操作
• np.sum() 可以直接把所有元素總和加總

• 對 的偏微分

  da = np.sum(x * (y_pred - y)) / n
  

• 對 的偏微分

  db = np.sum(y_pred - y) / n
  

有了偏微分的結果，那就可以去更新參數了。

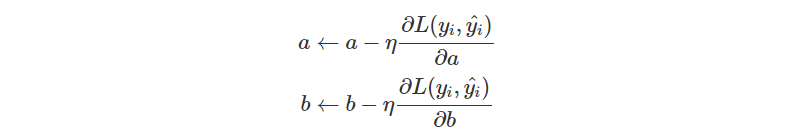
a = a - lr * da
b = b - lr * db

把整個更新流程整理整理，就是底下這個迴圈了！底下多了一個輸出，方便觀察運作是否正常。

for i in range(epochs):
    y_pred = a*x + b
    loss = Loss(y, y_pred)
    da = np.sum(x * (y_pred - y)) / n
    db = np.sum(y_pred - y) / n
    a = a - lr * da
    b = b - lr * db
    print(f'epoch {i}\tLoss: {loss}\ta: {a}\tb: {b}')

輸出結果成圖吧！

最後如果只是看到數字的話也許沒甚麼感覺，所以把結果畫在圖上看看吧！
這裡要使用的是 Matplotlib。

一開始先畫上資料點，由於只是點，所以對應到 scatter 這種畫圖方式。

import matplotlib.pyplot as plt
plt.scatter(x, y)

接下來再把預測出來的線畫出來，直接使用 plot 就可以了！

plt.plot([x for x in range(498, 2101)], [a*x + b for x in range(498, 2101)])

在 Matplotlib 當中要畫圖時很多時候都是給定兩個 list 分別表示 。

所以像是 scatter 就可以直接指定 和 這兩個 list。

而預測的直線則需要自己把 跟 找出來。由於資料的 範圍在 之間，因此這裡直接製作一個從 到 的 list。至於 的部分就只是單純把找出來的 套上 。

整體來說在畫圖的部分總結如下。

import matplotlib.pyplot as plt
plt.scatter(x, y)
plt.plot([x for x in range(498, 2101)], [a*x + b for x in range(498, 2101)])
plt.show()

epoch 999	Loss: 2445.6961741413174	a: 0.18974689200010145	b: 0.021732900571557866

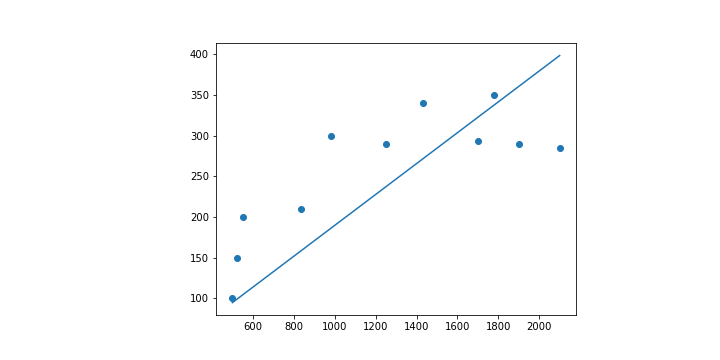
其實往往在訓練的過程當中我們也會想要去看整體的 Loss 究竟有沒有好好地減少，所以會把計算出來的 Loss 都記錄在一個 list 當中，並且也做成圖如下。

plt.plot([i for i in range(epochs)], Losses)
plt.show()

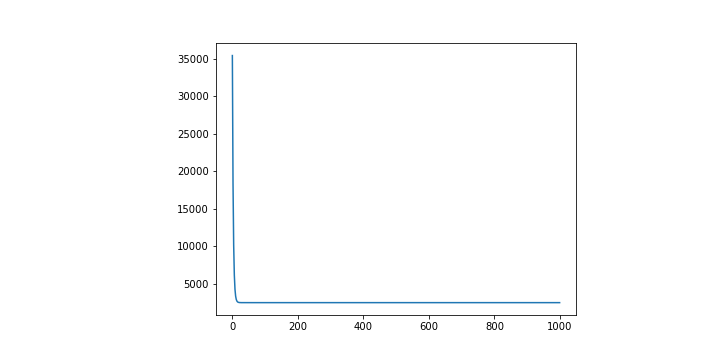
這是還蠻理想的狀況，能看到雖然一開始 Loss 相當大，但是隨著訓練，Loss 隨之變小。

這裡最終的 Code 就放在 Github 上，可以看看最終的樣子。

在成功之後

其實這一條線跟我在第二天舉的例子當中給的線是不一樣的。這一條線其實是用數學的方法直接求出來的直線，因為在這種簡單的線性迴歸其實算是簡單的問題。

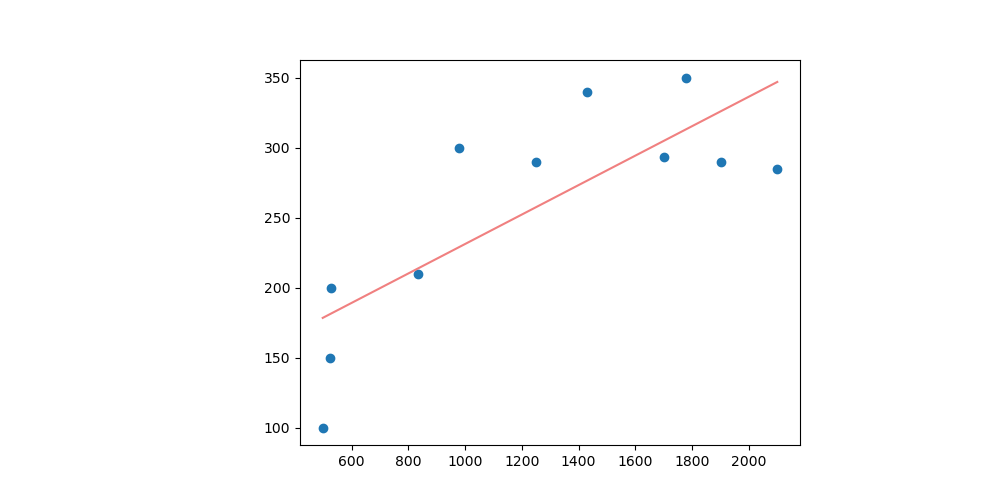
不過在成功以上面的程式執行完，看到很棒的 Regression 結果之後，你心中應該要存在一些疑問的。
因為在這個過程當中有很多突然告訴你這樣做的事情。舉例來說，參數的初始值。又或者是 Loss Function 乃至於模型的定義，為什麼要這樣做。

這些因素都會影響到最終模型呈現出來的結果。我們也許先把 Loss Function 以及模型定義放一邊，畢竟一開始就是想要討論比較簡單的狀況所以這樣設定，那麼其他這些參數的設定呢？

超參數 Hyperparameter 包含了 參數初始值 、 Learning Rate 和 epoch 都是會影響到最終模型長相的因素。
你可以試著調整看看這些參數，然後看看最終的結果有沒有什麼不一樣的地方。

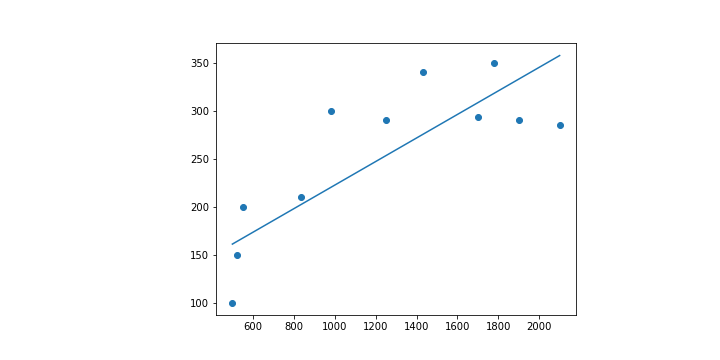
情境 1： 把初始值都設成 100，同樣的 code 會得到的 分別會是 和 。與上面的程式相比，他的線條比較向上，或是說 比較大。

情境 2： 激進一點把初始值都設定成 1000，同樣的 code 會得到的 會超乎想像的是 和 。
很奇怪吧，那甚至連斜率的正負都顛倒了。

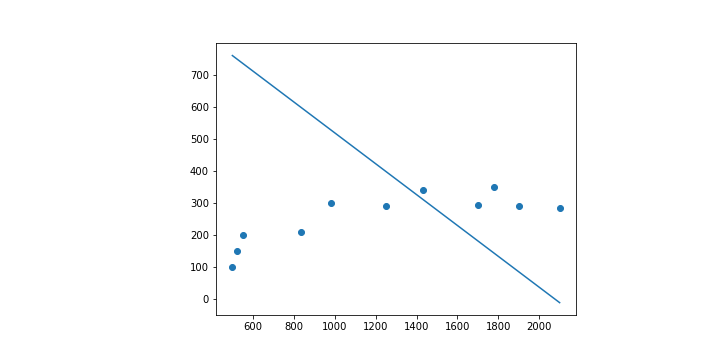
而且這個情況下的 Loss 居然是收斂的。

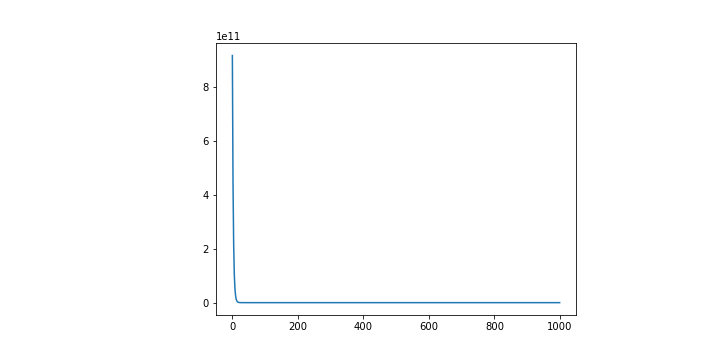
情境 3： 若是把原本的 code 的 Learning Rate 提高 10 倍。你會發現甚至會完全訓練不起來，因為 Loss 一直掉不下來。

欸，很奇怪吧。
前面我們明明提了那麼多，看起來也有數學佐證，為什麼會出現這樣的問題？

• 究竟該如何設定 Hyperparemeter？
• 究竟該如何檢查模型更新狀況好不好？
• ...

在這裡我們可以有很多很多的疑問想要提出，請先謹記並不是任意選一些數字，機器學習就會跟魔法一般完成一切，給你一個滿意的答案。

在後續的文章我們會更加深入提及這些問題，也希望透過這篇文章你能夠知道如何建構一個 Linear Regression Model，以及 Gradient Descent 的問題。